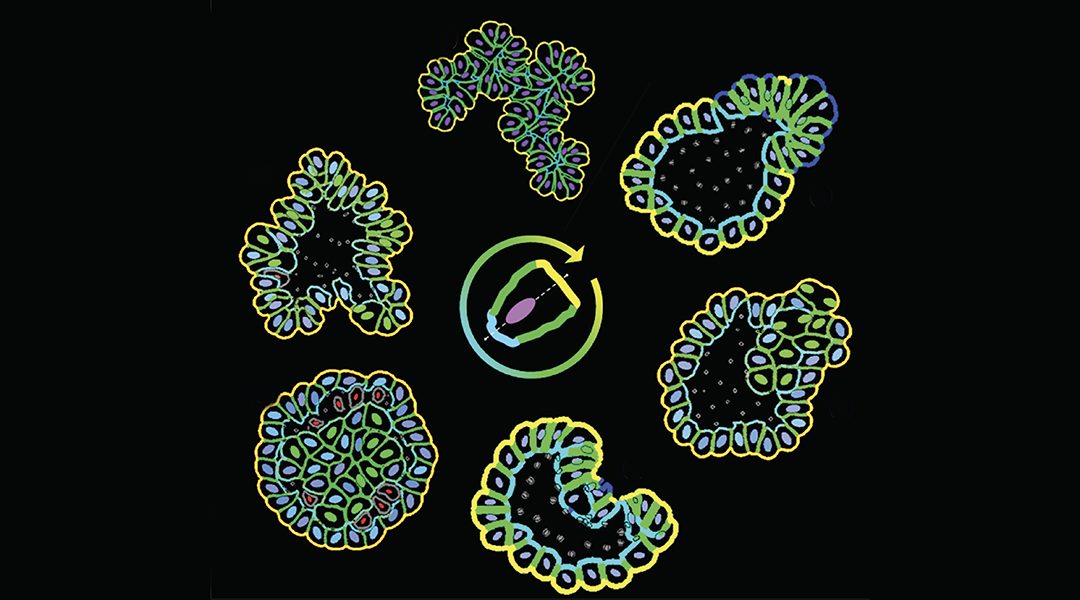
Cancer is a complex collection of diseases where no two tumors are alike, no two have developed in a similar way, and no two respond to therapy identically.
The initiation and progression of cancer is a multi-step process that depends on complicated interactions between the tumor, stromal cells, and the surrounding microenvironment. Therefore, cancer is a complex system comprised of various interacting and continuously changing components. In order to understand, analyze, and predict its behavior, advanced mathematical models are needed that can handle various types of information and combine diverse theoretical methods on multiple temporal and spatial scales, that is, hybrid models.
The word “hybrid” indicates that these modeling frameworks combine at least two different mathematical approaches. Classically, the discrete models that describe individual cells, each with potentially different characteristics, and the continuous models that describe concentrations of nutrients, waste products, and drugs, were coupled. However, in the last decade, advances in several new mathematical branches, such as machine learning, computer vision, fluid dynamics, optimal control, and optimal design, have enabled the incorporation of new methods in cancer modeling.
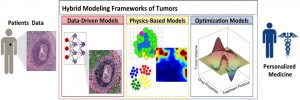
Hybrid modeling framework of cancer combines three classes of mathematical models: data‐driven, physics‐based, and optimization for development of a clinically relevant and quantitative decision‐making system for personalized medicine.
In a WIREs Systems Biology and Medicine review by Dr. Ibrahim Chamseddine and Dr. Katarzyna Rejniak, state of the art of mathematical hybrid modeling of cancer development and treatment are presented and three major modeling categories are identified: physics-based, data-driven, and optimization models.
“Hybrid modeling frameworks” are defined as techniques that combine models from any two of these categories. The paper discusses several modeling examples for each of the common anti-cancer treatments, including chemotherapy, targeted therapy, nanotherapy, hormone therapy, immunotherapy, radiation therapy, and combined therapy, and future research directions are proposed to enable the modeling of personalized treatments.
This study is addressed to both mathematical modelers, as a guide to the existing methods in cancer modeling, and to experimentalists, as a survey of anti-cancer therapies that were modeled in silico.
The integration of modeling and experimental approaches may allow the testing of a wide range of treatment strategies and the prediction of new, more personalized therapeutic protocols.