Traditional studies of materials have involved study of “bulk” materials and their various electronic and optical properties. However, as modern devices have shrunk in size to nanoscale dimensions, it has become increasingly important to understand the properties of materials at smaller dimensions and extents. The smallest materials systems currently studied are isolated nanoparticles. Experimentally and theoretically, their properties are rather well understood, just like the bulk materials.
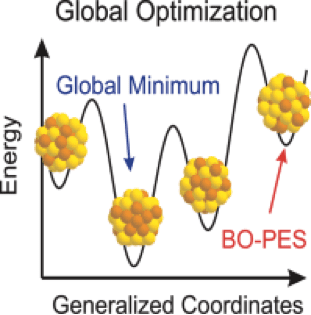
However, what happens at intermediate length scales is less well understood. At such length scales, quantum confinement effects are less pronounced but “surface” effects are still important. While semi-empirical methods exist, they are undesirable as they do not take into account the rich set of possibilities arising from chemistry and shape effects. Thus, it is desirable to develop ab initio methods for the intermediate length scales of materials (“clusters”). Computationally, this is a very complicated problem. The complexity of the overall optimization problem and the efficient modeling of the bonding are two basic problems for study of nanoclusters. Optimization typically proceeds through an exploration of a potential energy surface. As the cluster grows in size, the number of meta-stable isomers of the lowest energy state also increase rapidly. This puts paid to any prospects of doing a biased search based on basic bonding motifs.
In their review on global optimization of clusters, Sven Heiles and Roy Johnston explore this problem in detail. They present uses of genetic algorithms, basin hopping, etc. as examples of “classical” global optimization. Importantly, they then delve into first-principles global optimization and examine how genetic algorithms and basin hopping (among other methods) are modified. According to present state of development this new global optimization method is effective only for clusters with fewer than ~40 atoms.
The implementation and application of these search methods to allow exploration for global minimum cluster structures directly using electronic structure methods and, in particular, density functional theory is explored. Example applications are presented, ranging from isolated monometallic and bimetallic clusters to molecular clusters and ligated and surface supported metal clusters. The authors close with observations of the closing gap between empirical and first-principles global optimization methods.
—————
Related articles:
O. Anatole von Lilienfeld
Int. J. Quantum Chem. 2013, 113, 12, 1676-1689. DOI: 10.1002/qua.24375.