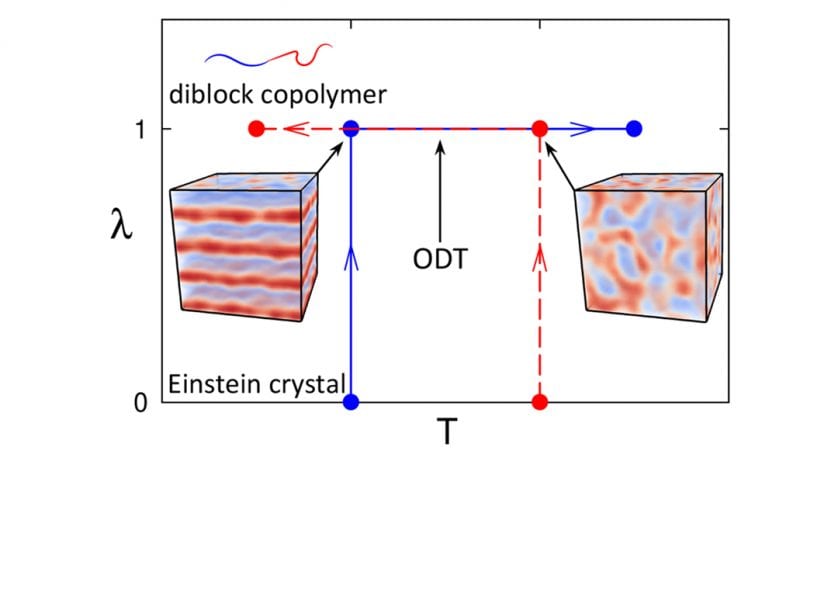
In their recent work, Russell Spencer and Mark Matsen (University of Waterloo) together with Bart Vorselaars (University of Lincoln) focus on simulations of diblock copolymers – a type of structured polymer, where one part of the molecule (a block) is composed of one type of monomer and the rest consists of another type (see Figure). A general incompatibility between unlike monomers causes the blocks to segregate into microscopic domains. The degree of segregation and structure of the domains depends on temperature. The challenge is to predict the order-disorder transition (ODT) temperature, which separates ordered structures (lamellar layers, for symmetric diblocks) from disorder.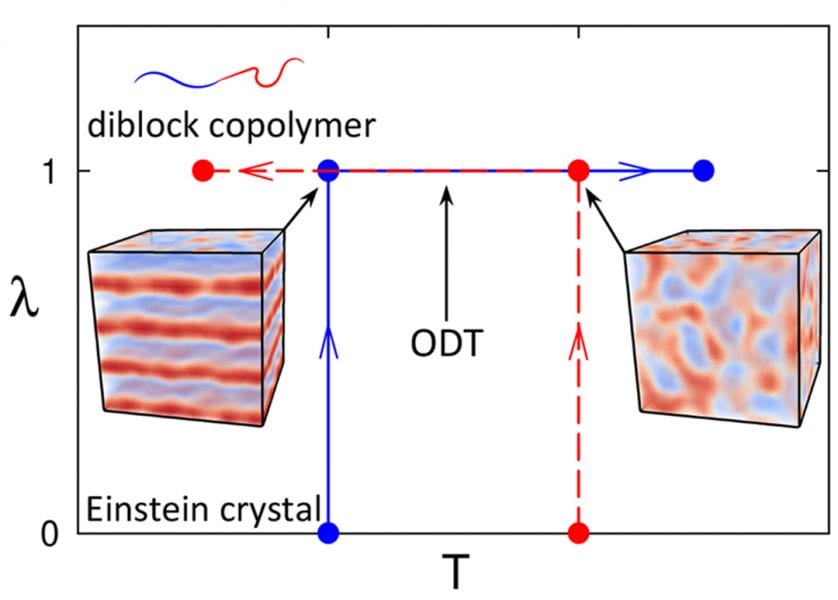
Standard particle-based simulation techniques represent each individual polymer in the system, which becomes very computationally expensive when molecules are long. This difficulty can be overcome by performing an exact mathematical transformation to a field-based representation involving a fluctuating field, controlled by an appropriate energy function. The technique is known as field-theoretic simulation (FTS), and becomes increasingly efficient as polymer length increases.
In principle, the simulations should converge to the stable ordered or disordered states, given sufficient time. The time required, however, becomes prohibitively long, close to the ODT, making it difficult to locate accurately. Alternatively, the ODT can be determined as the point where the ordered and disordered states have the same free energy. Simulations do not have direct access to free energies, nevertheless, they can calculate rates of change of free energies. These rates of change can be integrated to find free energy differences – a technique called thermodynamic integration. If there is a system with a known free energy (in this case, an Einstein crystal) that can be transformed into a system of block copolymers by changing a system parameter (λ), then the free energy can be integrated along λ to find the block copolymer free energy.
Thermodynamic integration is usually done discretely, by conducting many simulations at different values of λ, each finding a free energy derivative at that λ. The integral can be simplified by conducting one long simulation, continuously transforming the system from the reference state, λ = 0, to the block copolymer state, λ = 1. This continuous method is not only far simpler than the discrete procedure, but also allows for easy determination of statistical inaccuracies.