Nitroxide mediated polymerization (NMP) is considered to be a powerful and convenient macromolecular synthesis technique that belongs to the broader family of controlled radical polymerizations (CRP). These techniques exhibit the robustness of conventional free radical polymerization but behave similarly to living polymerizations, since they allow for chain extension (e.g., addition of a second monomer to form blocks) and for control of the molecular weight distribution. Among the CRP techniques available, NMP is one of the simplest to use and provides access to the synthesis of polymeric materials with controlled architectures, topologies and functionalities, while using environmentally friendly control agents.
When a copolymer synthesis is performed using any of the CRP techniques a natural question arises as to how the monomers are incorporated in the polymeric chain or, in other words, what are the rules that govern the addition sequence of monomers to the chain ?
The answer to this question determines the microstructure of the copolymer formed and whether the resulting structure of the copolymer will be alternating, gradient, or block. Furthermore, and more important from the perspective of the final use of the polymer, the resulting structure will have a dramatic effect on the properties of the material and its performance in applications. In conventional radical copolymerization, for most of the systems the monomer addition sequence and the copolymer composition are governed by the so-called terminal model and the corresponding copolymerization or Mayo-Lewis (ML) equation. This model postulates that the kinetics of addition of the next monomeric unit is determined only by the nature of the last unit previously added to the growing radical and its reactivity towards the monomers present in the system.
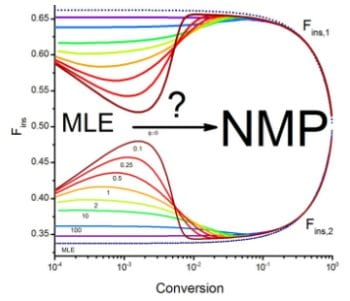
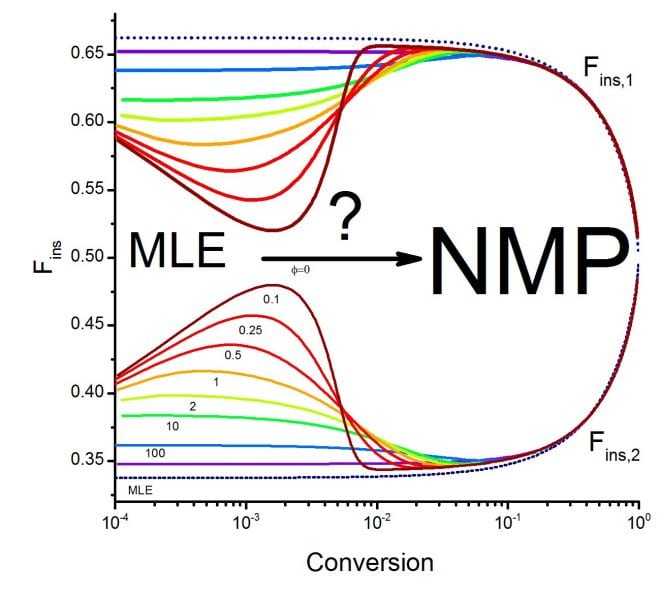
Previous works have shown that the copolymer composition in NMP and other CRP processes can in general be described by the terminal model (ML), but it is not clear if this is a valid generalization, especially because some works have reported small deviations of copolymer composition with respect to ML behavior in NMP and other CRP processes. If it is desired to use NMP for the synthesis of copolymers of controlled composition and architecture, it is important to understand the general behavior and the limits of applicability of the ML model in an NMP copolymerization system (or other CRP processes) and to answer some questions such as: What are the main mechanisms causing deviations of NMP copolymer composition data from ML predicted values?, and how do the copolymerization system kinetic parameters affect the extent of deviations?
The recent work by I. Zapata-González, E. Saldívar-Guerra, J. Ortiz-Cisneros (University A. de Coahuila and CIQA, Saltillo), R.A. Hutchinson (Queen’s University, Kingston) and K. Matyjaszewski (Carnegie Mellon University, Pittsburgh) addresses these and other relevant questions by a systematic analysis of NMP copolymerizations using kinetic simulations.
The results show that significant deviations from ML behavior occur in copolymer composition under various copolymerization parameter combinations during early steps of the reaction. Copolymerization systems with high reactivity ratios tend to produce more pronounced deviations from ML behavior, while those with low reactivity ratios, which result in a tendency to alternation (alternate collocation of monomeric units along the chain), are more likely to result in ML behavior. The presence of an additional continuous source of radicals in the system leads to a faster attainment of the quasi-equilibrium condition for the dormant-living species exchange, characteristic of NMP processes, and significantly reduces the deviations from ML behavior. This is a good example of a broader class of systems in which competitive chemical equilibria take place.
