The obvious importance of studying the direct link between a material’s structure and its properties is as true for polymers as for any other material, where the degree of branching alone can have drastic consequences on the potential applications of a single type of polymer. With the same chemical structure but very different densities, viscosities and tensile strengths, a case of mistaken identity between the low-density polyethylene used for plastic shopping bags and the high-density polyethylene used in heat-resistant piping, for example, could have interesting consequences.
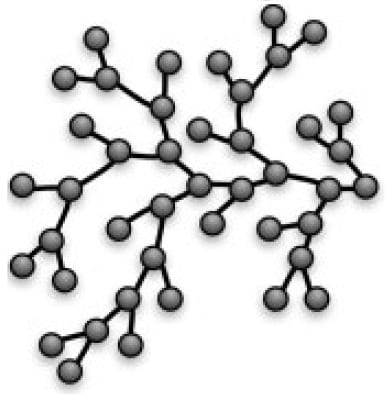
Structure optimisation for a specific application, or indeed the development of new materials with new properties, requires in the first place that a structure be predictable. The synthesis of regular, readily predictable structures such as dendrimers on the required scale for application involves multiple cycles of reaction and purification. Hyperbranched polymers, on the other hand – polymers along which the branches are randomly distributed – can be synthesised in a single step, but the final structures of such polymers assembled randomly from a collection of molecules of various identities and sizes are understandably difficult to predict.
To solve this problem, building on previous work, Konkolewicz et al. have developed ‘random branching theory’, which enables the modelling of the solution structure of randomly hyperbranched polymers. This model assumes that the polymers may be broken down into units of simpler structure (monomers, linear chains, or even spheres), of any size or chemistry, which have been assembled to form the final polymer structure.
This very flexible model assumes that the way in which the simple units are assembled is practically identical for all polymers. It determines the number of monomers per unit and their average size, and calculates the radius of gyration of each type of unit. It then examines the spatial density profile of the polymer at various degrees of polymerisation, which, for a given region, is proportional to the mass of the polymer in that region. If the polymer may be said to be built of N-1 sequentially added units, the model assesses the probability of the Nth unit being added at various distances from the polymer’s centre, with each attached unit considered a potential anchoring site for the next unit, thus building the density profile unit by unit. Contributions from steric hindrance of the units and even interactions with the solution can be taken into account.
After describing the model in detail, the authors then show the effects of mass scaling, the influence of each parameter of their random branching theory on the predicted polymer structure, and also how the model may be used as a test to determine whether or not a particular polymer is truly randomly hyperbranched.
