Quantum computers are definitely one of the hottest topics in modern information technology. With their theoretical advantages over classical computers, they have the potential to solve complex and out of reach problems. However, building a stable, functioning quantum computer has, to date, been very difficult, and experts worry that they may not yield the expected superiority — or quantum advantage — over their classical counterparts.
In a recent study published in Advanced Quantum Technologies, a group of physicists from Bar-Ilan University and Tel Aviv University tested modern state-of-the-art quantum computers with a set of algorithms they called “quantum games” to find out whether quantum advantage over conventional computers had been achieved in this specific type of problem-solving task.
Quantum computers rely on the laws of quantum mechanics, namely quantum entanglement and the principle of superposition. Superposition allows a qubit — the basic building block of a quantum computer — to exist as an arbitrary combination of both 0s and 1s, and entanglement links qubits together through subtle interactions to allow them to “work together”.
While these entangled, superimposed states lend quantum computers their superior capabilities, they are also extremely sensitive to external noise such that they can fall out of their superimposed states due to the tiniest outside influences. As a result, a functioning quantum computer has been hard to achieve.
In the current study, the team put a set of quantum computers to the test using a notorious nonlocal game in which quantum mechanics should have an advantage over classical theories.
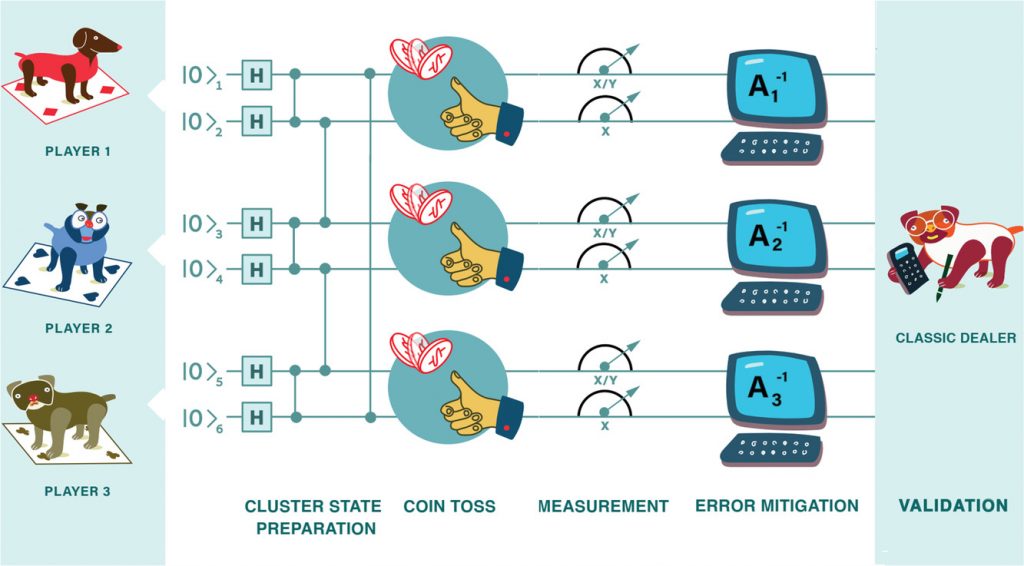
The game, referred to as the triangle game, requires three or more players to independently assign binary values to a set of variables, aiming to satisfy certain winning conditions. Each of these variables can be thought of as the choice between 0 and 1, or between heads or tails on a coin.
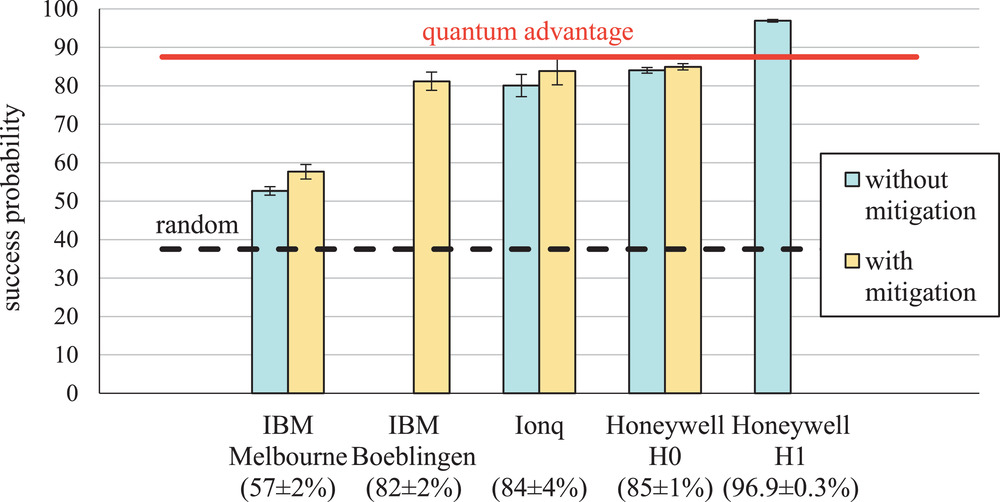
Even with the best strategy, these conditions can be satisfied, or a classical computer can “win” with an average probability of 87.5%. Whereas thanks to the entanglement between the variables, in the absence of noise, a quantum player should be able to satisfy all the conditions and win the game with a 100% probability. If players play randomly, the average winning probability is 37.5%.
The machines that authors bench marked in their study were IBM Melbourne and Boeblingen that have been built using superconducting qubits, as well as the trapped ion quantum computers, IonQ and Honeywell. All were prepared using a 6-qubit cluster state on the cloud.
The team found that only Honeywell H1 had a winning probability of about 97%, larger than the classical value of 87.5%, demonstrating a quantum advantage in this game, while the other four quantum computers failed to demonstrate their ability to beat the classical computers in solving problems of that type.
Interestingly, Honeywell H1 was the newest quantum computer among those tested in the study, and its success may reflect the steady improvement of quantum computers have made over time.
The scientists then took this a step further and played a more complicated game to see if the advantage was maintained. The classical winning probability in this game was around 67%, and surprisingly, the quantum algorithm implemented on the IonQ quantum computer achieved a winning probability of 87%. The authors haven’t tested the other quantum computers with this game, but they say they would expect them to deliver similar results.
An interesting question to explore, they say, is the demonstration of quantum advantage of various quantum computers with more complicated algorithms and with more entangled qubits.
Reference: Meron Sheffer et al., Playing Quantum Nonlocal Games with Six Noisy Qubits on the Cloud, Advanced Quantum Technologies (2022). DOI: 10.1002/qute.202100081
Feature image credit: FLY:D on Unsplash

















