The study of random copolymers remains an open and interesting field of research, due in part to the sheer enormity of the number of possible sequences. Here a generic model of random block copolymers is developed, in which each chain is modeled as a series of segments, the sequences of which are drawn from a distribution. The model is used to study the effects of blockiness and compositional dispersity on the phase behavior.
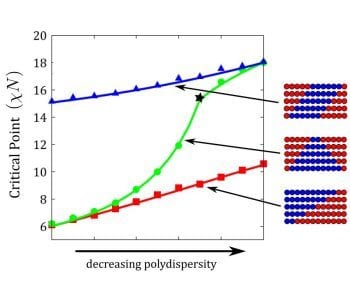
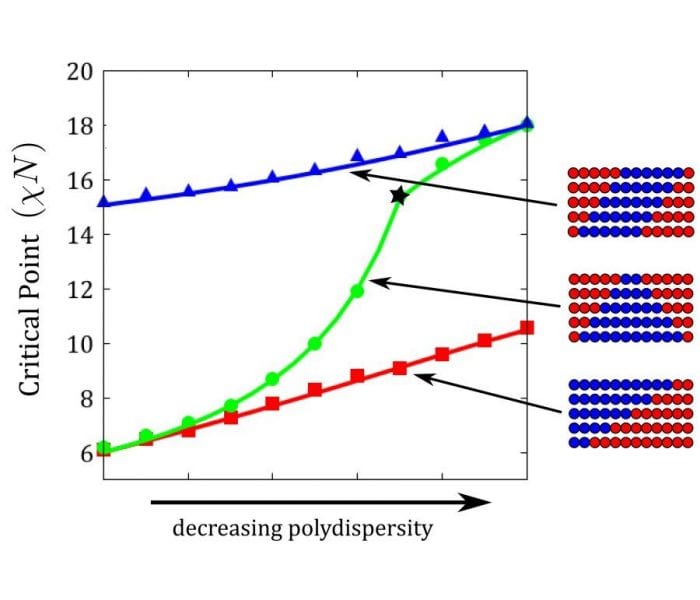
Random block copolymers remain an open topic of theoretical study due to the inherent complexity of the sequence distributions. In particular, the effects of blockiness on the phase behavior of random block copolymers have received less attention. In their present work, Gordon Vanderwoude and An-Chang Shi (McMaster University Hamilton, Canada) have developed a segment model of random block copolymers to study the effects of blockiness and compositional/sequential polydispersity on the order-disorder transition of the system. This top-down model begins with a deterministic approximation of the system based on the average blockiness, with the randomness introduced into it systematically bled from a collection of equal-length ‘segments’. The characteristics of the segments are chosen according to the nature of the polydispersity. The critical point of the system is calculated over a range of blockiness and polydispersity for a variety of segment models.
It is observed that the critical value of the Flory-Huggins parameter χ, above which the homogeneous phase becomes unstable, is inversely proportional to the blockiness. Furthermore, it is found that sequential and compositional dispersity decrease the critical value of χ, but that the effect of sequential dispersity is much weaker. At sufficiently large compositional dispersity, the random block copolymers could undergo macrophase separation.
