Forget about what you learned in school. In physics, and especially quantum physics, the average of a product of quantities can differ from the product of the averages of the individual quantities, i.e. is not necessarily equal . The difference is, by definition, due to correlations. Electronic correlations strongly influence the properties of matter. For example, they can induce a discontinuous transition from conducting to insulating behavior and thus are an ideal playground for physicists to explore fundamental aspects of solid state physics.
Dieter Vollhardt, recipient of the 2010 Max-Planck-Medal of the German Physical Society (DPG), has now summarized his insights on electronic correlations in the latest issue of Annalen der Physik, where he contributed to the prestigious Einstein Lecture Series. This series was established in 2005 in the course of the Einstein year and already consist of articles from Nobel laureates like Theodor Hänsch, Roy Glauber and Peter Grünberg. In his article Vollhardt discusses the theoretical description of correlated systems.
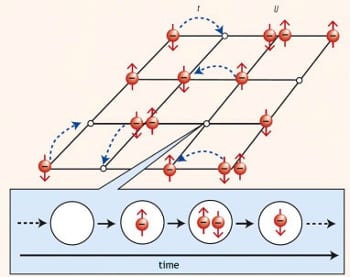
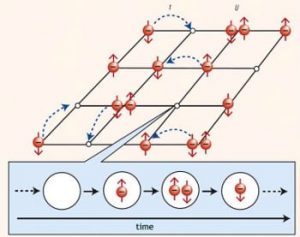
For many elements in the periodic table, two electrons occupying the same narrow d or f orbital (with opposite spin) are strongly correlated, since the effect of the Coulomb interaction between the electrons is enhanced by the spatial confinement. This applies for numerous materials with partially filled d and f electron shells, such as the transition metals vanadium and nickel and their oxides, or rare–earth metals.
The interplay between the spin, charge, and orbital degrees of freedom of the correlated d and f electrons with the lattice degrees of freedom leads to a wealth of correlation and ordering phenomena, which include heavy fermion behavior, high temperature superconductivity, colossal magnetoresistance, Mott metal-insulator transitions, and Fermi liquid instabilities. Such properties make materials with correlated electrons interesting not only for fundamental research but also for future technological applications, e.g., for the construction of tools such as sensors and switches and, more generally, for the development of electronic devices with novel functionalities.
In his work, Vollhardt describes the formulation of a comprehensive, non-perturbative many-body approach to correlated quantum many-body systems, the dynamical mean-field theory (DMFT). Over the last two decades the DMFT has developed into a powerful method for the investigation of electronic systems with strong correlations. It provides a comprehensive, non-perturbative and thermodynamically consistent approximation scheme for the investigation of finite-dimensional systems, and is particularly useful for the study of problems where perturbative approaches are inapplicable.
For this reason the DMFT has now become the standard mean-field theory for fermionic correlation problems. The generalization of this approach and its applications is currently a subject of active research. In particular, non-local generalizations of the DMFT play a major role. They will make it possible to study and explain even short range correlation effects which occur on the scale of several lattice constants. In 10 to 15 years from now DMFT-based approaches can be expected to be as successful and standardized as the presently available density functional methods. The development of a comprehensive theoretical approach which allows physicists to quantitatively understand and predict correlation effects in materials, ranging from complex anorganic materials all the way to biological systems, is one of the great challenges for theoretical physics.
