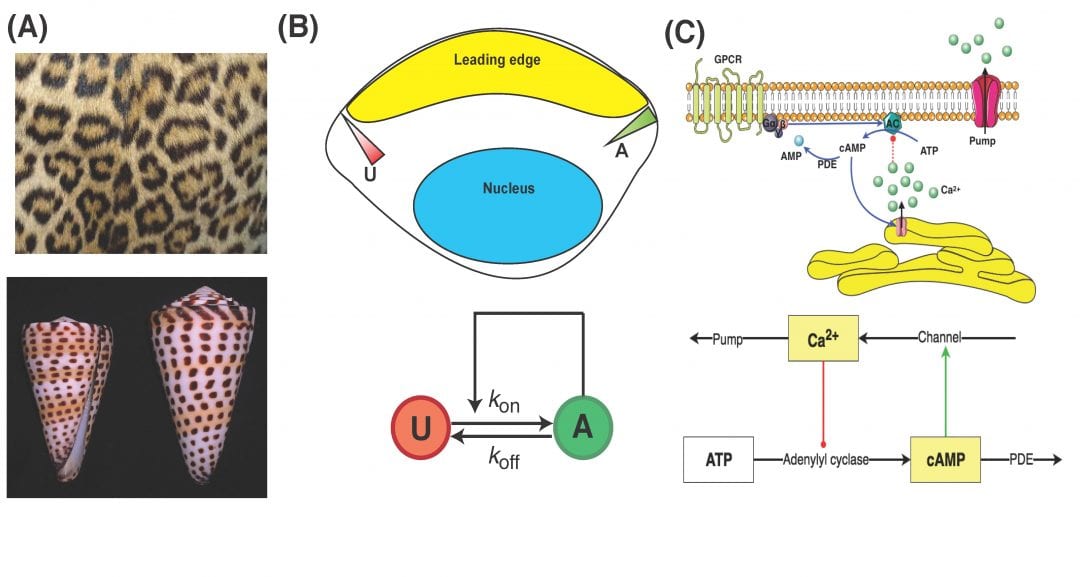
Due to advances in intracellular visualization techniques, the importance of the spatial segregation of signaling proteins has become more and more apparent. This separation can have myriad causes. Given the complexity of these systems, mathematical modeling is an ideal method with which to describe the observed spatio-temporal dynamics and generate experimentally testable predictions. Interestingly, similar models have been used to describe systems across many orders of magnitude in length and time: from signaling proteins within a cell  to the formation of stripes on a cheetah. These models allow us to further understand how such patterns can arise in the absence of any other known driving force.

So, why should you care about spatio-temporal dynamics? Why have we (and so many others) bothered modeling them? Well, in terms of the cell: Spatio-temporal activation profiles directly affect gene expression patterns, and different spatial organization can result in vastly different cellular responses. Furthermore, the localization of all the signaling components from initiation to completion impacts the final cellular response. Biochemical cascades, and other structured reaction pathways, have long been known to exhibit a large variety of purely temporal features, such as multi-stability and oscillatory behavior. However, modeling the system dynamics through the use of spatially-extended reaction-diffusion allows us to understand the spatial patterns that can arise due to diffusion effects as well.

So why haven’t we been doing this all along? While the analysis of temporal-only systems can be described by (relatively) easy to analyze ordinary differential equations (ODEs), the analysis of their spatial counterparts, partial differential equations (PDEs), is far more challenging. This Primer in WIREs Systems Biology and Medicine aims to guide the reader with a burgeoning interest in modeling spatially-organized biological systems through a basic understanding of the analysis of reaction-diffusion systems; in particular, what conditions allow for spatial patterning in simple systems. We provide methods in system analysis along with sample code to aid the reader and introduce them to the provided methods.

Kindly contributed by the Authors