A quantum system, isolated from the environment and initially in a single, “pure” quantum state, will evolve in time according to the Schrodinger equation, that is, it will remain in a pure state for all times. This is also true for a many-body quantum system. At first sight, this fundamental feature of quantum dynamics appears impossible to reconcile with experimental observations that show a sufficiently complex quantum system typically relaxes fast to thermal behavior if left on its own.
It constitutes the quantum thermalization problem. Of the huge amount of quantum numbers that characterize a complex quantum many-body state, only a small subset can be measured in any realistic experiment. Thus, the measurement process itself divides the system into a subsystem of measured quantum numbers and a state space spanned by all the undetermined quantum numbers. The latter are averaged over and thus comprise a grand canonical heat bath for the measured subsystem. Therefore, under very general conditions, the subsystem thermalizes, completely consistent with the total system remaining in a pure quantum state for all times.
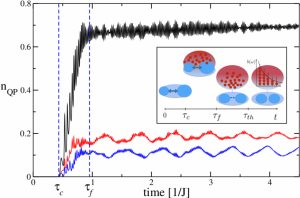
Total density of incoherent excitations (black), and their density in the first (red) and second (blue) excited trap levels.
Anna Posazhennikova from Royal Holloway University of London, UK Mauricio Trujillo–Martinez and Johann Kroha from the University of Bonn, Germany have now shown in their review, published in Annalen der Physik, that this thermalization mechanism even holds when the heat bath states are initially not populated. In this case, the system dynamics itself populates and, hence, generates the heat bath.
In contrast to effective bath techniques, this group of researchers compute the quantum dynamics of the complete system, comprised of subsystem as well as entangled bath quantum states, using quantum many-body techniques. In this way, they are able to trace the path a system takes to the thermal state, when the heat bath has its own non-Markovian quantum dynamics.
As a concrete example, they consider a Bose–Einstein condensate (BEC) trapped in a small double-well potential. They identify three stages associated with the bath generation process, initially undamped, quantum-coherent BEC oscillations (Josephson oscillations), followed by a period of avalanche-like creation of incoherent excitations far from equilibrium (population of bath states)and a crossover to a hydrodynamic regime with slow relaxation to thermodynamic equilibrium driven by quasiparticle collisions. The figure shows the three regimes for the total density of incoherent excitations (black) and for their density in the first (red) and second (blue) excited trap levels.

















