Image credit: Sina Katirachi Unsplash

It is a rare occurrence in solid-state chemistry and condensed matter physics to discover an entirely new class of materials that never existed before. Even more unusual is the discovery of a new materials property. Topological solids fall into this category of solid-state materials discoveries, and materials chemists are in the throes of trying to understand the new physics that will underpin the new chemistry this unique class of materials foretells.

The story begins with the discovery of a class of crystalline solids with an electronic band structure that by design creates high-mobility electrons. What is special about these electrons is they are situated in the surface of the solid, protected from and invisible to interactions with the underlying bulk, and are invulnerable to various kinds of crystal imperfections (e.g., dopants and defects). This recently uncovered class of materials are dubbed “topological solids”. Imagine the opportunities for exploiting surface confined electrons in the field of heterogeneous catalysis!

In the context of chemistry and physics, topology is the hallmark of all known crystalline materials, discussed in terms of the real space positions and local symmetry of atoms in the primitive unit cell, the overall symmetry of the unit cell and the crystal structure. Unsurprisingly, topology therefore determines the electronic band structures of all known crystalline metals, semiconductors, insulators, semi-metals and superconductors. The advent of topological solids introduces an electronically distinctive class of materials to the field of solid-state chemistry and physics.

A natural question in the physics of this class of materials, is how many of all known materials in the world can be classed as topological solids? This is not an easy question to answer as the physics underpinning topological materials is complex and deciphering the basic concepts and principles in the framework of chemistry is challenging.

In simple terms, a topological insulator is a material with a small electronic bandgap, an insulating core, and an electrically conducting surface. By contrast, a topological semi-metal is similar but bandgap-less. To put this novel concept into a solid framework, the figure below depicts the chronological timeline of recent discoveries of topological solids, beginning with the archetype 2D Dirac topological insulator and extending to the 3D Dirac, Weyl, and most recently, Nodal line semimetals. For these different classes of topological solids, examples of materials compositions and their respective, so-called, non-trivial band structures are also provided.

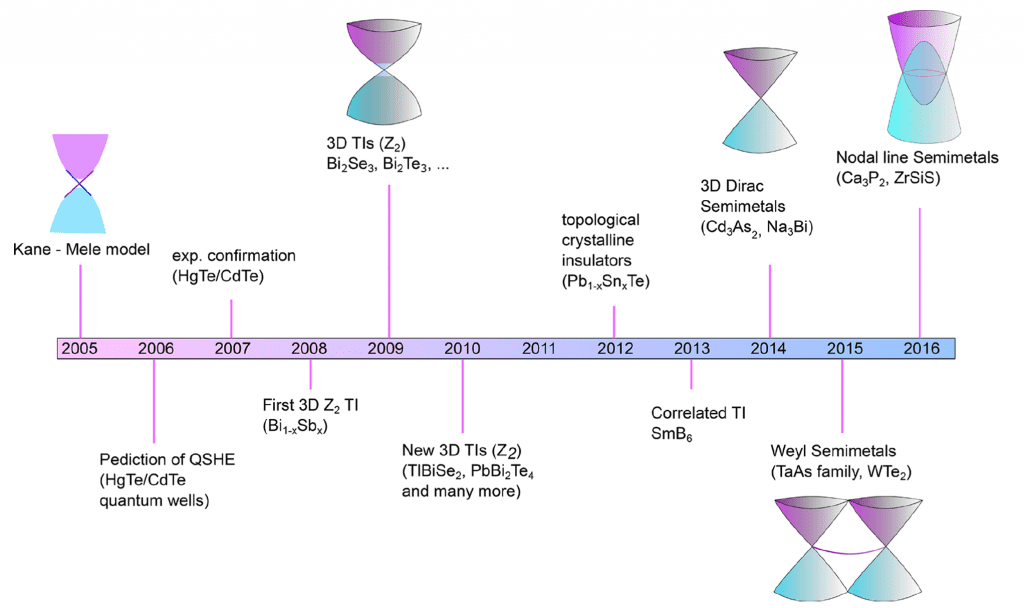
Early studies of topological insulators focused on 3D binary and ternary bismuth, antimony, and mercury chalcogenides. In this class of solids, the Fermi level (i.e., the energy of the least tightly bound electrons) resides in the bandgap between the filled valence and empty conduction electronic bands of the bulk. Two linearly dispersed topological surface states cross at a Dirac point near the Fermi level and in three-dimensions take the shape of the upper and lower halves of a conical surface, the so-called Dirac cone, a signature feature of a topological material.

These states are responsible for the high surface electrical conductivity. The states are separated off and robustly decoupled from the normal bulk conduction and valence band states. As a result, the carrier mobility of the surface electrons is exceptionally high, and moreover, invisible to the bulk and resistant to the deleterious resistive scattering and localization/trapping losses caused by various kinds of bulk imperfections.

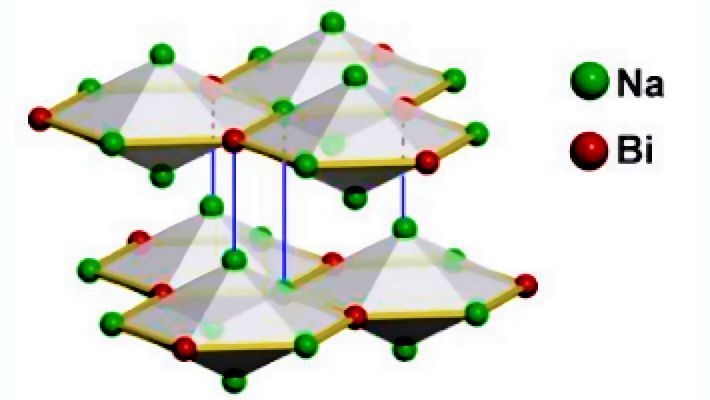
An example of a 3D topological semi-metal is sodium bismuthide, Na₃Bi. It has an interconnected layered structure, which can be viewed as a 3D inorganic analogue of graphene and exhibits the properties of a gapless Dirac semi-metal. In this material, two linearly dispersed surface states also cross at a Dirac point to form a Dirac cone.

In the language of chemistry, it is believed that the inversion of the energies of the relativistic 6s² lone pair of electrons with the 5d¹⁰ filled-shell electrons on the Bi(III), causes this unique band structure of Na₃Bi to form, rather than the one with a normal parabolic-shaped valence and conduction band structure. This class of gapless topological semi-metals are characterized by the Dirac band crossing, yet the nature of their surface states and their protection seems less apparent than in topological insulators.

While the physics and emergent electrical, optical, and magnetic properties of each of these topological solids is distinct to non-topological ones and the subject of very active investigation, fascinating questions are being asked and exciting opportunities pertain to the chemistry that could be enabled by the special properties of surface confined electrons.  

This is where topological materials and surface confined electrons enter the story of heterogeneous thermochemical, electrochemical, and photochemical CO₂ catalysis, because the performance of a heterogeneous catalyst depends on optimizing the reactivity of a gaseous or liquid reagent with the surface of a catalytically active solid either in an unsupported or supported form.

Because these chemical reactions depend upon surface adsorption, interfacial charge-transfer and transport, surface chemistry and desorption, one can anticipate that understanding and exploiting the reactivity of electrons at the surface of topological solids will prove to be of considerable interest in catalysis, whether a heterogeneous reaction is driven by heat, electricity, light or a combination thereof.

Although quite sparse, some reports of topological catalysis are beginning to appear in the literature for topological carbon monoxide oxidation, water splitting, and carbon dioxide catalysis, in a search for the “topological advantage”, if any, over non-topological analogues. The challenge faced in these pioneering studies has been to disentangle the innumerable geometric, electronic, and support effects that normally contribute to heterogeneous catalysis from the special effects of topology, most credibly and realistically performed under operando experimental conditions. Making a convincing case that topology really contributes to catalysis instead of just co-existing with it, will be a very difficult yet worthwhile undertaking.

Clearly, this is an exciting time for the discovery of topological materials in the fields of electronics, optics, magnetics, and catalysis. Already many reports are emerging that use artificial intelligence and machine learning in large-scale searches for compositions, structures and symmetries that can host the topological state. Thirteen years ago at the conception phase of the field of topological materials, it was generally believed that only a minute fraction of known materials would exhibit the exotic signature properties of the topological state. Surprisingly, recent theoretical studies showed 25-27% of all known materials can be described as topological in nature.

In one of these investigations, all high-quality stoichiometric materials in the 26,938 Inorganic Crystal Structure Database were computed in a high throughput search using a topological quantum chemistry formalism. This approach links the topology of a material to its crystal symmetry and employs the convention of elementary band representations (EBRs) to decide whether the compatibility and connectivity rules of bands in the Brillouin zone are satisfied. From this investigation topological materials could be distinguished from non-topological ones, resulting in the discovery of 3,307 and 4078 topological insulators and semi-metals, respectively. An open-source code now provides researchers with the ability to make general searches of the electronic properties of all topological materials. 

Clearly, solid-state physicists and materials chemists are now in excellent “shape” to expand and accelerate their explorations of the science of topological materials for a wide range of possible applications.

Geoffery Ozin

Solar Fuels Group, University of Toronto Ontario, Canada, Email: [email protected], Web sites: www.nanowizard.info, www.solarfuels.utoronto.ca, www.artnanoinnovations.com

References:

Schoop, Leslie M., Florian Pielnhofer, and Bettina V. Lotsch. Chemical principles of topological semimetals, Chemistry of Materials (2018). DOI: 10.1021/acs.chemmater.7b05133

Klemenz, Sebastian, et al. The role of delocalized chemical bonding in square-net-based topological semimetals, Journal of the American Chemical Society (2020). DOI: 10.1021/jacs.0c01227

Liu, Z.K., et al., Discovery of a three-dimensional topological Dirac semi-metal, Na₃B., Science (2014). DOI: 10.1126/science.1245085

Bradlyn, Barry, et al., Topological quantum chemistry, Nature (2017). DOI: 10.1038/nature23268

Zhang, Tiantian, et al., Catalogue of topological electronic materials, Nature (2019). DOI: 10.1038/s41586-019-0944-6

Liu, Pengzi, James R. Williams, and Judy J. Cha, Topological nanomaterials, Nature Reviews Materials (2019). DOI: 10.1038/s41578-019-0113-4

Gibney, Elizabeth, Thousands of exotic ‘topological’ materials discovered through sweeping search, Nature (2018). DOI: 10.1038/d41586-018-05913-4

Vergniory, M. G., et al., A complete catalogue of high-quality topological materials, Nature (2019). DOI: 10.1038/s41586-019-0954-4