Correlations in many-body systems can be extraordinary, particularly those with a quantum origin. Consider the (in)famous exchange correlations resulting from the quantum indistinguishability of particles. These can be very obvious. For example, the Pauli exclusion principle prevents condensation of ordinary fermion systems in the low temperature limit. Furthermore, it induces exchange holes causing ordinary fermions to “avoid each other” (i.e., it is unlikely to find them in a close proximity). Thus, analytical and numerical methods revealing correlations in many-body systems are needed and desired, even when they require recognized many-body wave functions, Ψ.

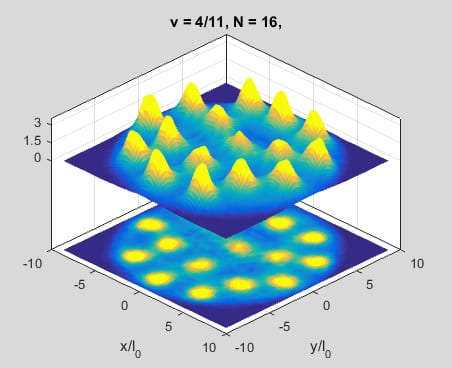
Exchange-correlation holes are commonly studied with the help of pair distribution functions. However, it would be instructive to identify configurations of arguments, λ, which correspond to maxima of system’s probability distributions. Especially, if it was possible to recognize how selective they are (i.e., how likely the most probable λ are). These can be studied with the help of configuration probability distributions, whose method of a numerical evaluation is introduced in a paper recently published. The method combines a Simulated Annealing algorithm and a modified Metropolis Monte Carlo scheme (with a carefully selected angular orientation of each generated configuration of arguments).

The usefulness of configuration probability distributions is verified in integer and fractional quantum Hall systems comprising up to sixty particles. The most probable λ of Laughlin states are found to resemble classical Wigner crystals. Simultaneously, the most probable λ on non-Laughlin states are different and establish complicated geometric structures (i.e., classical non-Wigner crystals). The many-body wave functions considered in the work are concluded from the topological approach based on the idea of restricting the exchange correlations to subsets of particles (i.e., the idea of removing the homotopy classes from braid groups). Finally, it is demonstrated that configuration probability distributions allow to classify internal orders of integer and fractional quantum Hall systems and explain peculiarities of their transport measurements.