Electronic devices take advantage of the conduction properties of individual elements within an integrated circuit, by combining them to produce some desired effect. In the last decades, such devices have been continually miniaturized to improve portability and efficiency, and reduce power consumption. Nowadays, such reduction in size has reached nanometric scales, where quantum effects become important. For example, interference phenomena caused by the wavelike behavior of electrons, imply that the effect of individual components depends on the properties of other elements present in the device, making it a complex system.
Theoretically, such systems can be studied trough the so-called S-matrix, in the context of scattering theory, which relates the incident and outgoing waves affected by a physical system. In other words, the S-matrix contains all the information of the effect of a system on the transmission of a wave or particle onto its surroundings, which are modeled by leads that may represent the connection to classical (macroscopic) systems, such as electrodes. Within the context of Landauer-Büttiker formalism, it is possible to study conductivity by using parameters of the S-matrix. However, calculation of the S-matrix has been considered computationally expensive for large systems. For this reason, physical quantities directly calculable by using the S-matrix are commonly obtained from other related quantities such as the Green function, which frequently reduces calculation efficiency. For example, density of states can be easily computed from the S-matrix. In contrast, it requires using all diagonal elements when computed from the Green function matrix, and consequently the computational time increases rapidly for large systems.
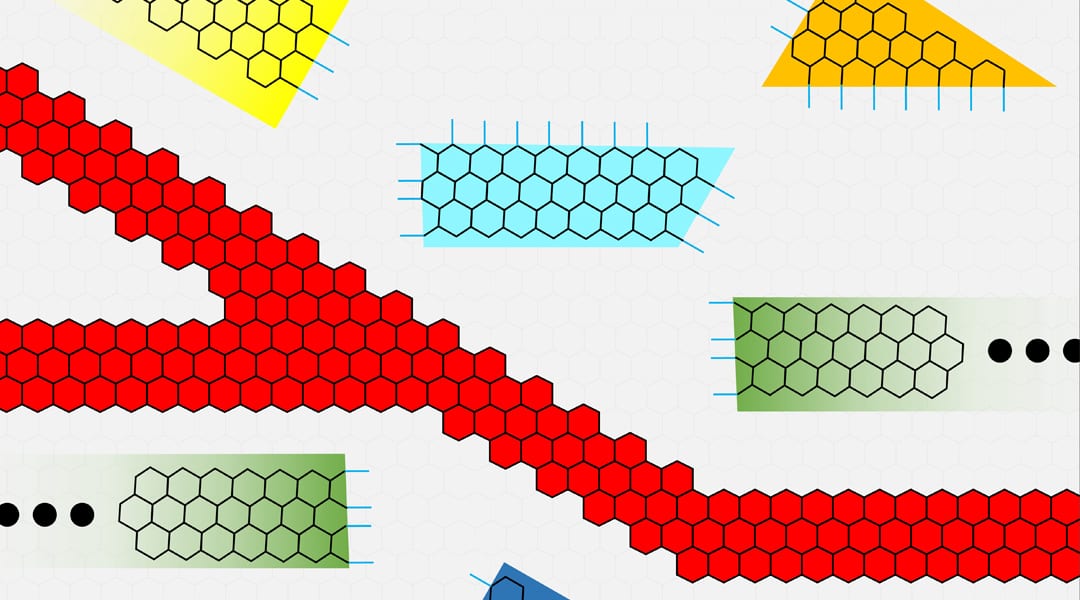
In a recent article published in Annalen der Physik, Carlos Ramírez at Universidad Nacional Autónoma de México proposes a highly efficient method to determine the S-matrix of systems modeled by tight-binding Hamiltonians with general leads. In this method, the S-matrices of small subsystems are analytically calculated and then joined iteratively, along with its effects, as building blocks to form larger arbitrary systems. This assembly process allows the exploration of conductivity in large complex devices, including infinite periodic ones and can be used, for example, to study conductivity in nanodevices composed entirely of graphene nanoribbons, where different arrangements and geometries are easily realizable.