Interacting quantum systems can show quasi-periodic, non-ergodic dynamics if the interaction of their components (spins or particles) is sufficiently small. This regime is similar to the celebrated Anderson localization, describing metal-dielectric transitions; nevertheless this localization is of substantially many-body character. Many-body localized systems possess long-term memory of the initial quantum state and highly coherent dynamics, which is needed for functioning of modern quantum computing devices. Yet, many-body localization is not completely understood.
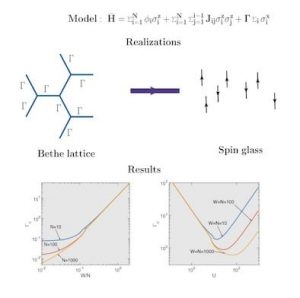Numerical methods are applicable to relatively small systems of 15-20 particles because of the exponential growth of the number of quantum states with the system size. Therefore the development of analytical theories is significant, and the step toward such development is proposed by Dr. Alexander Burin in Annalen der Physik. The accurate solution of the many-body localization problem is reported for the Sherrington- Kirkpatrick spin glass model describing spins 1/2 placed in random longitudinal fields and coupled by binary spin-spin interactions. The small transverse field induces dynamics and the system gets delocalized when this field exceeds the critical value, i. e. the localization threshold. This localization threshold is determined using the matching problem of the localization transition in random graphs (Bethe lattice). The delocalization can be described as the sequence of transitions of resonant spins (having small longitudinal fields). These transitions can switch resonances of other spins by means of changing their longitudinal fields, which eventually results in irreversible dynamics. Depending on the interspin interactions, delocalization can be induced by resonant spins in the strong interaction case or by spin pairs in the case of a weak interaction.
The results are extendable to other systems of interest ranging from interacting electrons in quantum dots to interacting electronic or nuclear spins coupled by power law interactions. The theory can be tested experimentally for spin excitations in cold atoms and semiconductors.
The text is kindly provided by Dr.Alexander Burin.
The article will be published in the forthcoming special issue Many-Body Localization
(Guest Editors: Jens H. Bardarson, Frank Pollmann, Ulrich Schneider, Shivaji Sondhi)
